¿Cómo enseñar fractales a los niños?
Grrrrrrr!!!!!!!
Saludos.
Cada cierto tiempo, y debio a la diálectica misma de la vida, surgen nuevas áreas el conocimiento que se vuelven parte de la cultura general de los ciuadanos del siglo XXI. Un tema ausente en los currículos educativos nacionales el Perú (hasta diciembre e 2013) es el de los fractales.
El reto de los maestros es el de inducir estos conceptos a los alumnos de corta edad ¿cómo podriamos iniciar a los niños de 7, 8 o 9 años en las nociones de fractales?
Esta figura es un fractal. Un fractal es una figura, cualquier figura, que se repite un número infinito de veces.
Hace tres años atrás (2005) asumí este reto y como resultado elaboré un blog para mis alumnos de tercer y cuarto grado. Decidí enfocar la geometría desde diversos ángulo: observando, descubriendo, recortando, asombrandose... y relacionando la geometría con aplicaciones prácticas y con el deleite estético (la geometría con el arte).En el caso concreto de los fractales considero que no hay manera más sencilla de iniciar a los alumnos que a través de la curva de Koch. ¡Con ustedes la curva de Koch!
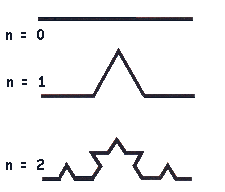
Y así sucesivamente. Otro modelo interesante es el de la Isla de Koch:
Finalmente les dejo la figura de Sierpinski...
Y finalmente unas ideas para realizar con sus alumnos:
¿Qué tal? ¡Interesante! ¿No es cierto?
Esta es una buena idera para realizar con los niños: crear un fractal con latas vacías. Aquí les dejo los pasos básicos para elaborara una impresionanate figura de Sierpinski. ¡Atentos! Vía: De Mates ¿Na?
¿Cómo elaborar una figura der Sierpinski?
Paso 1. El primer paso no reviste ninguna dificultad: consiste simplemente en pegar tres botes de refresco formando un triángulo equilátero. Pero, ¡ojo! hay que tener la precaución de echar la silicona en la cantidad y el lugar adecuados. Después los sujetaremos con una goma elástica para evitar que se nos muevan antes de secarse la silicona.
(3 botes utilizados)
+ + = 
(9 botes utilizados)
Paso 3: Necesitamos tres “triángulos” del paso 2 ya secos para, siguiendo la línea del paso anterior, pegarlos formando un nuevo “triángulo” equilátero. Obtenemos así un “triángulo” con ocho botes por lado que habrá que mover con sumo cuidado si está recién pegado, para que no se desmorone.
+ + =
(27 botes utilizados)
Paso 4. Como vemos la dinámica es siempre la misma: partir de tres triángulos del paso anterior –perfectamente pegados y secos– para pegarlos después, aunque no de cualquier modo, formando un nuevo “triángulo” equilátero. Aquí empleamos ya… ¡81 botes!
+ + = 
(81 botes utilizados)
Los pasos 3 y 4 son de mayor dificultad (por si acaso). Pero el pegamento de "SILICONA" ayuda mucho en los procesos de construcción e nuestra figura.
El resultado: IMPRESIONANTE:
En el siguiente video ustedes encontrarán una nueva manera de enfocar la figura de Sierponski, una manera divertida pero con rigor matemático. Además es una estupenda forma de visualizar la multiplicación de fracciones. (Video en inglés).
Más información en:
Fractales (para niños)
Blog Polígonos1
Blog Polígonos2
La gran figura de Sierpinski
BONUS: También se pueen elaborar fractales en tercera dimensión empleando tijeras y papel estos videos nos dan una idea de cómo construirlos. ¡Manos a la obra!
Los abrazo fuerte con mis garras...
Leonardo Sánchez Coello
El León Mayor
Fractales (para niños)
Blog Polígonos1
Blog Polígonos2
La gran figura de Sierpinski
BONUS: También se pueen elaborar fractales en tercera dimensión empleando tijeras y papel estos videos nos dan una idea de cómo construirlos. ¡Manos a la obra!
Los abrazo fuerte con mis garras...
Leonardo Sánchez Coello
El León Mayor
5 rugidos:
WOWWWW
sensacional, ud si que capacita mejor que esos cursos de chang.
de donde saca tiempo ud para investigar tanto en internet, mis respetos.
siga ud adelante.
Xeverengue!
Your blog keeps getting better and better! Your older articles are not as good as newer ones you have a lot more creativity and originality now keep it up!
Thank you. The education is my passion.
Leo (from Peru)
Publicar un comentario